nyaaaaaaaaaaaaa  I’m sick now
I’m sick now
it’s going around
At a table with my friends and comparing orgo grades and one says she did “really bad” and isn’t disclosing her grade and is talking about how terrible she did. It is revealed that she did not get a B, except “metaphorically”. She is asked if she got an A. Eventually she breaks down and admits she got an A, but it was worse than the other guy’s 112. And then says it was better than my 108. But this is “really bad”
We’re trying to talk about apartments but we were getting really offtopic and were talking about the hello training and my ex and he was asking who it was and when he was informed he said “damn you hit that” and hten was immediately extremely mebarrassed that he said it
We’re fermenting maple syrup. She has a maple syrup nutritional yeast creatine concoction also that shse’s drinking
NYAAAAAAAAAAAAAAAAAA just solved this
time to find out if my solution is right
NYAAAAAAAAAAAAAAA nvm I think I assumed something bad thtbhtbthbthbthtbt time to check before watching
fishing. metaphorically speaking.
Purrr
I FIGURED IT OUT
it?
oh right.
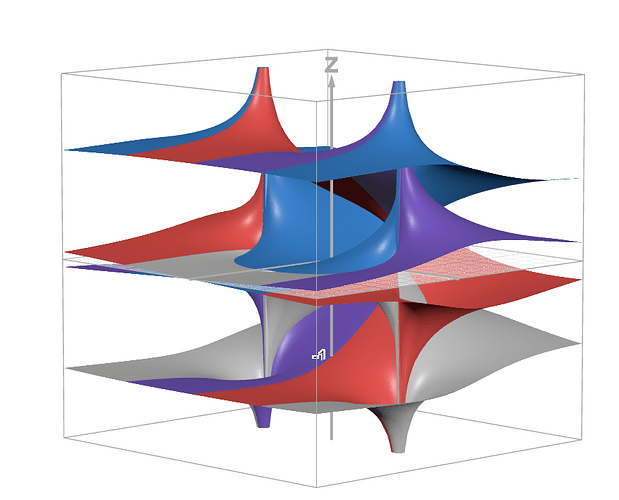
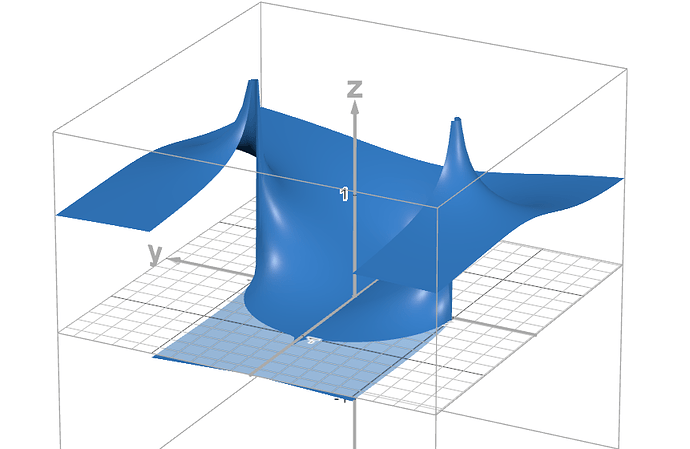
Okay, so we’ve got this complex function. It maps one 2d complex number z to four 2d complex values f(z). Here’s a shitty visualisation of the real part of this function:
Basically there’s a “parking garage” situation, if you go in circles around certain points you’ll go up or down a layer.
You can turn this multi-valued function into a single-valued one by making “branch cuts”, basically saying “here’s a line in the parking garage I won’t cross so that I stay on the same layer this whole time”. These branch cuts should be around branch points, the “centres” of that parking garage around which you can change layers. Each branch point creates a discontinuity in the function, it’s a little “jump” where the parking garage abruptly goes from one floor to the other, like this:
My task was to create branch cuts on tihs function, with branch points at (1,0), (0,1), and (0,-1), that kept hte function continuous on the real axis and in the circle of radius 2 centred around the origin.
Usually, you want your branch cuts to be straight lines connecting the branch points so that their little “jumps” line up and the function doesn’t “jump” more than it has to. If two branch cuts facing each other meet, you can make them “cancel out” so that they only create that little jump on the line between the two, not extending off infinitely into the distance. So I initially thought to set up my cuts like this:
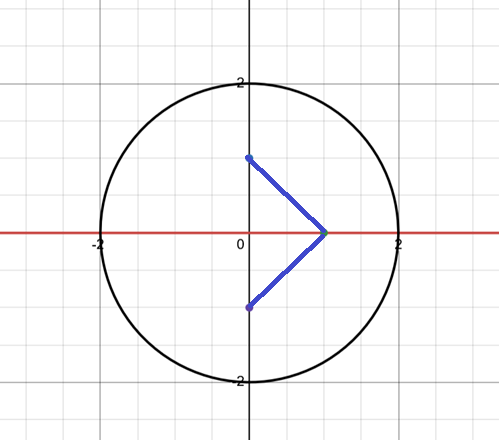
See, the cuts are lined up so that they connect the dots. However, since there’s 3 points, this creates a problem: the branch cut for (1,0) has to face either toward (0,-1) or (0,1), it can’t face both at once, and that means the other cut extends off into infinity, creating a discontinuity in the circle.
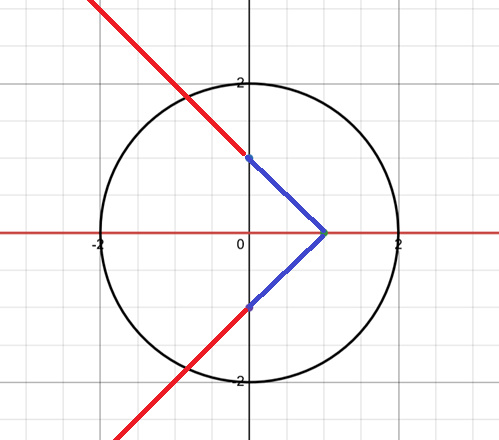
I’ve been thinking about how to make the right cuts for days, since we’ve only ever been presented with problems with two branch points before. And while I was lying there at 3AM I came up with the right answer:
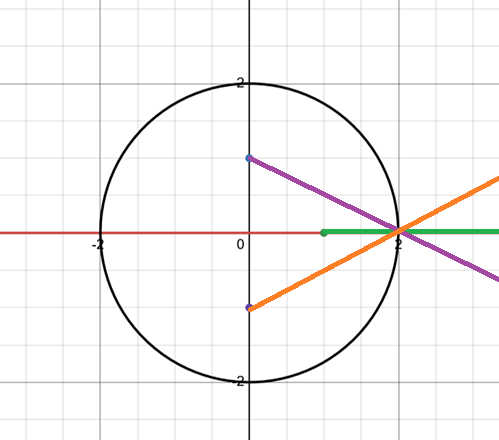
These branch cuts don’t cancel out. They create annoying discontinuities extending to infinity. Except on the real axis and the circle. They create a dumb stupid messy branch, but it’s one that’s continuous on the requested area, so it’s correct. And that’s my branch cuts
And the fucking problem is that the TA, who is mildly ot majorly stupid, marked that initial answer with the shitty branch cuts as correct on my initial try at the exam when I’m pretty sure those branch cuts can’t be made in a way that’s continuous in the right way. So like
NYAAAAAAAAAAAAAAAAAAAAAAAAA what’s the function
also I cant say we’ve done much with branch cuts tbthbthtbthbthtbhtbhtb
the only branch cuts we’ve done are for logarithms